これはパイロクロア酸化物Dy2Ti2O7（参考文献）を舞台とした面白いスピン系の話です。

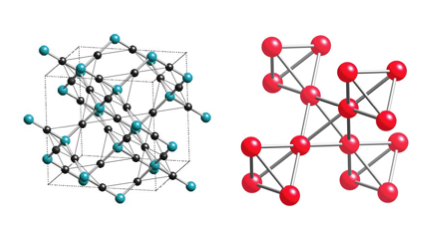
パイロクロア酸化物の構造はCd2Re2O7の超伝導においても示してありますが、こちらはDy/Cdサイトに注目します。下図左にはDy原子を黒球で、これを繋ぐ酸素原子を水色球で示してあります。ここからDy原子のみを取り出すと下図右のように、Cd2Re2O7のRe格子の場合と同様にパイロクロア格子が現れます。

Dy2Ti2O7ではDy3+イオンが局在性の強いｆ電子からくる大きな磁気モーメント（10ボーアマグネトン）を持っています。一方、Ti4+にはｄ電子がいないので、Cd2Re2O7のように伝導電子は存在せず、ばりばりの絶縁体です。よって、ここで問題にするのはDyスピンの自由度であり、このパイロクロア格子上のスピン系が低温で如何にエントロピーを放出して、どのような基底状態に落ち着くかに興味が持たれます。

さて、スピン系の秩序化に重要なのはスピンの異方性とスピン間の相互作用です。Dy3+の場合、スピンの異方性は極めて大きくイジングスピン、つまり、上向き・下向きの２つの状態しか取れません。また、その向きはDy四面体の中心かその反対向きを取ることがわかっています。一方、最近接スピン間の有効的な磁気相互作用は強磁性的でその大きさは約１Ｋと見積もられています。

世の中には賢い人がいて、このスピン系を氷の構造と関係付けて議論しました。

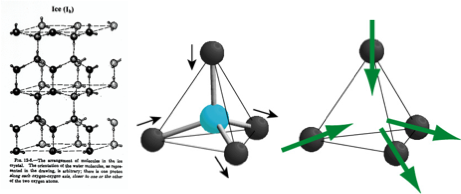
左下図に六方晶氷の結晶構造を示します。そこでは酸素イオンがダイヤモンド類似の格子を組み、２つの隣接する酸素イオン間に一つの水素イオンが存在します。よって１つの酸素イオンは４つの水素イオンによって囲まれており、水素イオンの４面体の中心に位置するとみなすことが出来ます。しかし、ここで氷がH2O分子の集まりであることを考えると、４つの水素イオンのうち２つが近づいて化学結合を作り、残りの２つが遠ざかって隣の酸素イオンに属することになります。

60年以上前にLinus Paulingは面白いことに気が付きました。氷が出来る過程において、各水素４面体につき、どの２つの水素イオンが選ばれるかに自由度があり、これは4Ｃ2=６通りあります（中下図）。さらに１つの４面体で水素イオンの位置を決めても、お隣の４面体にはまだ自由度が残り、これを無数の４面体が３次元的に繋がった氷で考えると、巨視的な自由度が残されることになります。水素イオンの位置には２つのポテンシャルミニマムがあるわけですから、その位置に関する全エントロピーは、水素イオン１モル当たりRln2(5.76 J/K mol)で与えられ、熱力学第３法則（絶対零度ではエントロピーがゼロ）に従うと、このすべてのエントロピーが絶対零度で解放されなければなりません。しかしながらPaulingの見積によると、水素イオン１モルあたり(R/2)ln(3/2)(1.69 J/K mol)のエントロピーが残されることになります。これを残留エントロピーとかゼロ点エントロピーと呼びます。一見、熱力学第３法則が破られたかに見えますが、そんなはずはなく、どこかにトリックが隠されています？

この不思議な氷の残留エントロピーの問題は実験的に取り扱うことは難しく、長年の間、置き去られてきましたが、そこで登場するのがパイロクロア酸化物です。もし、水素イオンの位置にイジングスピンがあり、四面体の中心かその反対のみを向く二つの状態しか取れないとすると（右下図参照）、その向きが水素イオンの位置に関する自由度と等価になります。さらに、四つのスピンのうち二つが内向き、二つが外向きのスピン配置が安定であるならば、これはまさに氷の問題と一致することがわかります。 Dyスピンは確かにこのようなイジングスピンであり、また、強磁性的な相互作用は右下図のようなtwo-in,two-out構造を安定化します。

このようにスピン系はしばしば、その他の系のモデル物質を与えます。スピン系における実験を通してその本質に迫ることが可能となります。さらにスピン系では外部磁場を制御することにより系のエネルギー状態を自由に変化させて実験を行うことが可能となります。

では、Dy2Ti2O7に戻りましょう。

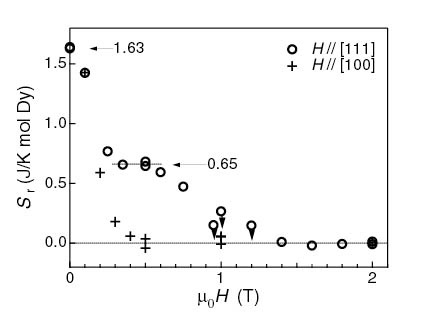
下図はDy2Ti2O7単結晶を用いて比熱を測定し、そこから求めた残留エントロピーの磁場依存性（参考文献）を示したものです。ゼロ磁場では確かにPaulingが予測した値とほぼ一致した残留エントロピーが得られています。ここで結晶の[100]方向に磁場をかけるとマクロな縮退が解け、残留エントロピーがゼロになります。これは磁場によるゼーマンエネルギーによってすべての四面体で１種類のtwo-in, two-out構造が安定化されるためです。

面白いのは[111]方向に磁場をかけたときに見つかりました。この時は[100]方向の場合とは異なり、残留エントロピーはあっさりゼロにならず、途中の磁場強度でプラトーを示します。その時の残留エントロピーはゼロ磁場の約４０％となっています。

この中間状態が、カゴメアイス状態です。

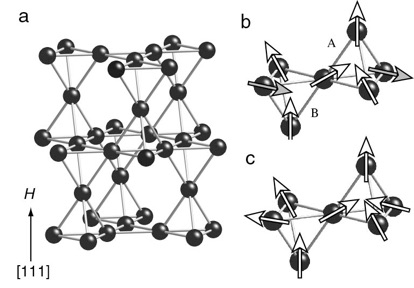
パイロクロア格子を[111]方向に垂直に眺めると、下図ａのように、原子が密な面と粗な面が交互に積み重なっていることがわかります。今度は[111]方向から眺めると前者は下下図のようにカゴメ格子（各正三角形の頂点がDy）をなし、後者は３角格子を取っていることがわかります。２つの隣接する四面体を抜き出してみると、下図ｂのように、カゴメ面内のスピンは磁場（[111]方向）に対して傾いており、残りのスピンは四面体の上下の頂点にあって僅かな磁場でもその方向にピンされることが予想されます。この時、四面体Ａではすでに外向きのスピンを一つ持っており、四面体Ｂではすでに内向きのスピンを一つ持っていることになります。よってtwo-in, two-out配列が満たされるためには、前者のカゴメスピンにはin-in-outの、後者のそれにはin-out-outの新たな規則が適用されます。頂点スピンにはもはや自由度はありませんが、カゴメ面内のスピンにはまだ自由度が残っていることになります。対応する残留エントロピーは宇田川、小形（参考文献）によって厳密に計算されており、実験とほぼ一致することが確かめられています。

このような中間状態をカゴメアイスと名付けました。これは磁場によってスピン系の次元性を三次元から二次元に変化させたことに対応します。カゴメアイスの残留エントロピーは明らかにカゴメ格子の特殊性から来ています。

さて、さらに磁場を強くするとすべてのスピンが磁場方向に成分をもつ、one-in, three-out、または、three-in, one-out状態（下図ｃ）が安定化されて、すべてのエントロピーが失われます。この時の変化が一次転移であり、非常にドラマチックであることが最近わかってきました。これはガス状態のカゴメアイスから、液体状態への特異な気体ー液体転移であり、スピン系では初めての例と思われます。この相転移は絶対零度近くでも起こると予想されており、大変興味深いものです。今後の実験の進展が楽しみです。

最後に、残留エントロピーの問題ですが、熱力学第三法則が成立しない理由は二つ考えられます。菅宏先生の解説によると、一つは測定が行われた最低温度より低い温度域で、弱い相互作用による比熱異常が測定し残されている可能性です。もう一つは、限られた測定時間のために真の平衡状態にない系について実験が行われ、乱れた構造が測定時間内に凍結したままであることに起因します。スピンアイスでは、スピン間の有効相互作用は１Ｋ程度と見積もられており、これより十分低い温度（数十ｍＫ）までの測定で比熱に異常は見つかっていません。よって、前者の可能性は低いと思われます。一方、氷の残留エントロピーの問題と同様、スピンアイスでは我々が制御し得ない時間スケールが深く係わっていることは明白です。スピンアイスの研究を通して、熱力学への理解を少し深めることが出来ました。Ｚ